ZHANGKB

【算法】如何分析算法的时间复杂度

2023/03/29 11:36:31

分析时间复杂度的方法

  1. 只关注代码中执行次数最多的部分。
  2. 总复杂度等于量级最大的那段代码的复杂度。
  3. 嵌套代码的复杂度等于嵌套内外代码复杂度的乘积。

只关注代码中执行次数最多的部分

function total(n) {
  var sum = 0;
  for (var i = 0; i < n; i++) {
    sum += i;
  }
}

这个函数中执行最多的部分为 for 循环中的语句，共执行了 n 次，所以这段代码的时间复杂度为 O(n)。

总复杂度等于量级最大的那段代码的复杂度

如果一段代码中包含多个不同时间复杂度的代码，那么总的时间复杂度取数量级最高的那部分，并且忽略常数项。

function total(n) {
  // 第一个 for 循环
  var sum1 = 0;
  for (var i = 0; i < n; i++) {
    for (var j = 0; j < n; j++) {
      sum1 = sum1 + i + j;
    }
  }
  // 第二个 for 循环
  var sum2 = 0;
  for (var i = 0; i < 1000; i++) {
    sum2 = sum2 + i;
  }
  // 第三个 for 循环
  var sum3 = 0;
  for (var i = 0; i < n; i++) {
    sum3 = sum3 + i;
  }
}

第一段 for 循环的时间复杂度为 O(n2)O(n^2)。

第二段 for 循环的执行次数与 n 无关，时间复杂度为 O(1)。

第三段 for 循环的时间复杂度为 O(n)。

所以总的时间复杂度为 O(n) + O(1) + O(n2)O(n^2)，取最大数量级的部分也就是O(n2)O(n^2)。

嵌套代码的复杂度等于嵌套内外代码复杂度的乘积

function fn(i) {
  var sum = 0;
  for (var j = 0; j < i; j++) {
    sum += j;
  }
  return sum;
}
function total(n) {
  var res = 0;
  for (var i = 0; i < n; i++) {
    res = res + fn(i); // 调用 fn 函数
  }
}

total 函数的时间复杂度为 T1(n) = O(n)，fn 函数的时间复杂度为 T2(n) = O(n)。

因为在 total 函数中调用了 n 次 fn 函数，所以总的时间复杂度为 T(n)=T1(n)∗T2(n)=O(n∗n)=O(n2)T(n) = T1(n) * T2(n) = O(n*n) = O(n^2)。

常见的时间复杂度分析

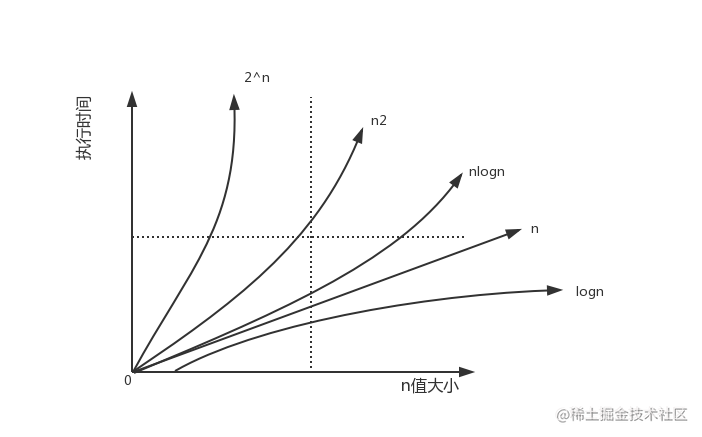
下图中时间复杂度的效率是递减的：

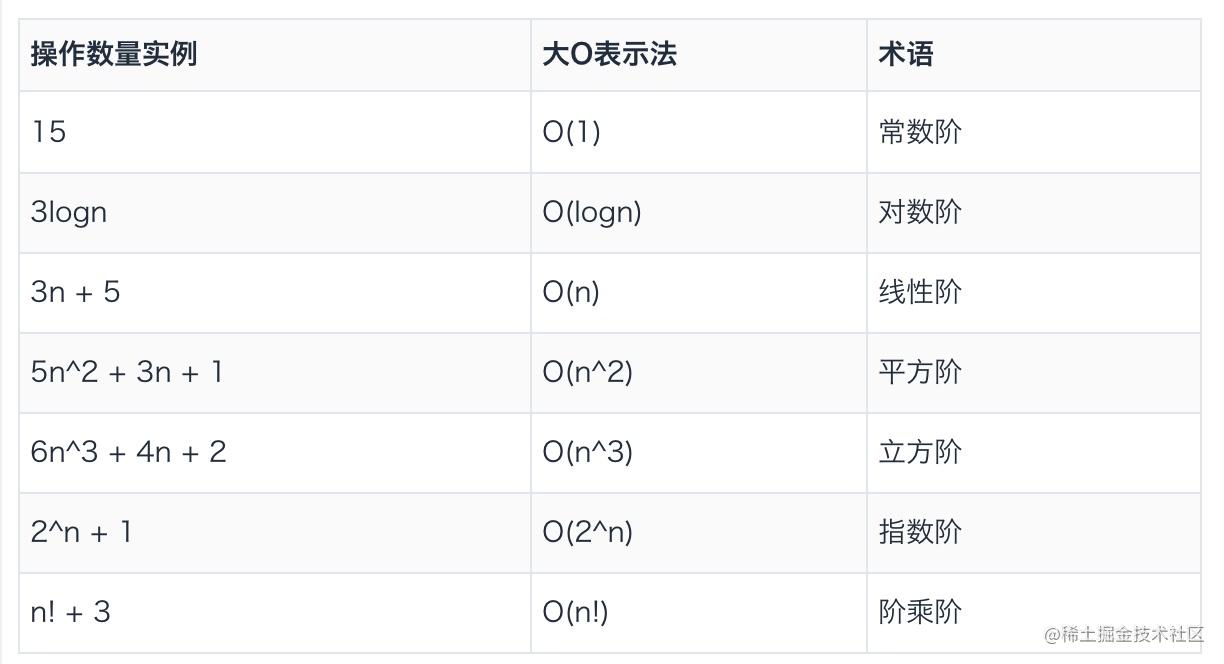
常见的时间复杂度

对应的图表展示为：

常见时间复杂度的效率

O(1)

代码的执行时间不随 n 的增大而增长，这样的代码时间复杂度为 O(1)

function total() {
  var sum = 0;
  for (var i = 0; i < 100; i++) {
    sum += i;
  }
}

O(logn)、O(nlogn)

对数阶时间复杂度的常见代码如下：

function total1(n) {
  var sum = 0;
  var i = 1;
  while (i <= n) {
    sum += i;
    i = i * 2;
  }
}

变量 i 从 1 开始取值，每循环一次乘以 2，当大于 n 时，循环结束。实际上，i 的取值就是一个等比数列，就像下面这样：

20,21,22...2x=n; 2^0, 2^1, 2^2... 2^x = n;

只要知道 x 的值，就可以知道这两个函数的执行次数了。由 2x=n2^x = n 可以得出 x=log2nx = log_2n，所以上面函数的时间复杂度为 O(log2n)O(log_2n)。

下面这个函数的时间复杂度为 O(log3n)O(log_3n)

function total1(n) {
  var sum = 0;
  var i = 1;
  while (i <= n) {
    sum += i;
    i = i * 3;
  }
}

由于我们可以忽略常数，也可以忽略对数中的底数，所以在对数阶复杂度中，统一表示为 O(logn)；O(nlogn)O(nlogn)的含义就很明确了：时间复杂度为 O(logn) 的代码执行了 n 次。

O(m + n)、O(m * n)

function total(m, n) {
  var sum1 = 0;
  for (var i = 0; i < n; i++) {
    sum1 += i;
  }
  var sum2 = 0;
  for (var i = 0; i < m; i++) {
    sum2 += i;
  }
  return sum1 + sum2;
}

因为我们无法评估 m 和 n 谁的量级比较大，所以就不能忽略掉其中一个，这个函数的复杂度是有两个数据的量级来决定的，所以此函数的时间复杂度为 O(m+n)；那么 O(m*n) 的时间复杂度类似。

参考

JavaScript 算法之复杂度分析open in new window